システムスループット、 Fナンバー、開口数

レンズのFナンバー (f/#) 設定は、全体的な透過光量 (スループット) や被写界深度 (DOF)、また特定空間周波数におけるコントラスト生成能力を制御します。Fナンバーは、理論的にはレンズの開口径$ \small{ \left( \varnothing _{\text{EA}} \right) } $に対する焦点距離 $ \small{\left( f \right)} $の比で求められます。

(1)$$ \text{f}/\# = \frac{f}{ \varnothing _{\text{EA}}} $$

(1)

$$ \text{f}/\# = \frac{f}{Ø_{\text{EA}}} $$

大抵のレンズでは、Fナンバーは絞り調節用リングを回すことで調節できます (レンズの構造参照)。レンズ内部に搭載したアイリス絞りの開口を開いたり、閉じたりすることで行います。リング部に書かれたFナンバーの数字は、その開口径によって得られるレンズの透過光量の大きさを表します。その数字は、通常$ \sqrt{2} $倍の大きさ毎に段階的に増加していきます。Fナンバーが$ \sqrt{2} $倍増えると (即ち隣の数字に上がると)、絞りの開口の大きさが半分になり、レンズの透過光量を1/2に減らします。Fナンバーの低いレンズは、｢明るいレンズ｣を意味し、より多くの光をシステム内に取り込むことを可能にします。これに対して、同ナンバーの高いレンズは、｢暗いレンズ｣を意味し、少ない光量を取り込むことを意味します。Table 1は、焦点距離 25mmのレンズに関するFナンバーや開口径、及び実質的な開口面積を紹介した一例です。F1からF2に移動した時の開口径と開口面積の大きさの変化や、F4からF8への同パラメータの大きさの変化にご注目ください。開口径は½の大きさになり、開口面積は1/4の大きさに変わることがわかります。レンズのFナンバーが増えることで、透過光量がどう減っていくのかがこの一例からおわかりいただけると思います。

Fナンバー	レンズ開口径 (mm)	開口面積 (mm²)
1	25.0	490.8
1.4	17.9	251.6
2	12.5	122.7
2.8	8.9	62.2
4	6.3	31.2
5.6	4.5	15.9
8	3.1	7.5

Table 1: f=25mmの単レンズに関するFナンバーと開口面積の関係： Fナンバーの大きさが増えると、開口面積の大きさが小さくなり、透過光量のより少ないイメージングシステムになっていく

Fナンバーによるレンズの解像力、コントラスト、被写界深度への影響

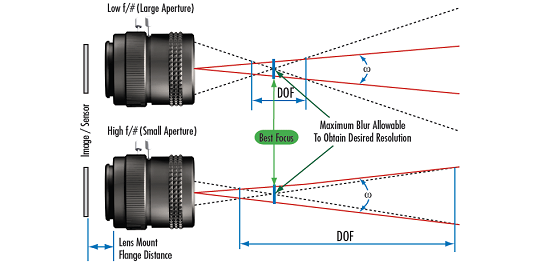
Fナンバーは、透過光量の大きさだけでなく、別のパラメータにも影響を及ぼします。特に、レンズの理論的な解像力やコントラスト限界、及び被写界深度 (DOF) や焦点深度に直接的に関係します (DOFに関する更なる情報は被写界深度と焦点深度を参照)。Fナンバーは、特定レンズデザインの光学的収差にも影響を及ぼします。センサーの画素サイズがどんどん小さくなっている昨今、Fナンバーはシステム性能を決定付ける最も重要な制限因子の一つになっています。というのは、Fナンバーによって被写界深度と解像力の性能が相反する方向に働くからです。Table 2は、画質に関する各種パラメータ全てを同時に改善することが不可能で、アプリケーションに応じて何らかのパラメータを妥協していかなければならないことを端的に表わしています。

Fナンバー	回折限界時の解像力	被写界深度	透過光量	開口数 (NA)
	$Diffraction Limited Resolution Performance Changes$

Table 2: Fナンバーが変化すると、レンズ性能も変わる

Fナンバーは作動距離の変化に伴い変わる

公式1に紹介したFナンバーの定義は、作動距離 (撮影距離) が無限遠、即ち光学倍率的には実質ゼロ倍の場面に限定されたものです。大抵のマシンビジョンアプリケーションにおいて、物体はレンズに対して無限遠よりも遥かに短い距離に実際配置されています。この時のFナンバー、即ち有効Fナンバー (f/#)_wは、大抵のアプリケーションにおいてより有益なFナンバーとなり、公式2 を用いて求められます。

(2)$$ \left( \text{f}/ \# \right)_w \approx \left( 1 + m \right) \times \left( \text{f}/ \# \right)$$

(2)

$$ \left( \text{f}/ \# \right)_w \approx \left( 1 + m \right) \times \left( \text{f}/ \# \right)$$

(f/#)_wに関する公式において、mは光学倍率 (レンズにより得られる像高の物高に対する比) を表わします。この公式で、mがゼロに近づく (即ち物体の位置が無限遠の距離に近づく) と、(f/#)_wは無限遠時に定義されたf/#に近づいていくことに注目ください。より小さな作動距離で考える際は、無限遠時に定義されたf/#ではなく、(f/#)_wを考えていくことがとても重要です。例えば、F2.8のf=25mmレンズを0.5Xの倍率で使用する時、実質的な(f/#)_wは4.2になります。この値がレンズの集光能力同様、画質にも影響を及ぼします。

Fナンバーと開口数

レンズの全体的な透過光量について検討する際、レンズが光を取り込むことのできる最大角度 (最大推角)、即ち開口数 (Numerical Aperture; NA)の概念から考えた方がよりわかりやすい場合があります。レンズの開口数 (NA)は、像空間側での周辺光線 (Marginal Ray)の正弦関数で定義し、Figure 1の図のθの正弦関数で表わされます。

Visual representation of f/#, both for a simple lens (a), and a real-world system (b).

Figure 1: 単レンズ (a)と現実的なシステム (b)各々におけるFナンバーの視覚的再現

Fナンバー (f/#)とNAには、反比例の関係があることにも理解しておくことが重要です。

(3)$$ \text{NA} = \frac{1}{2 \times \left( \text{f}/\# \right)}$$

(3)

$$ \text{NA} = \frac{1}{2 \times \left( \text{f}/\# \right)}$$

Table 3は、レンズの絞りリングに書かれた代表的なFナンバー値 ($ \sqrt{2} $倍毎にステップ)と、それに対応する開口数の関係を表わします。

f/#	1.4	2	2.8	4	5.6	8	11	16
NA	0.36	0.25	0.18	0.13	0.09	0.06	0.05	0.03

Table 3: FナンバーとNAの関係

全体透過光量の大きさを表すのに、顕微鏡学ではFナンバーの代わりにNAが一般的に用いられますが、顕微鏡用対物レンズで規定されるNAの値は、物空間側で規定されていることを理解しておくことが重要です。Fナンバーが解像力にどのような影響を及ぼすかについての詳細は、MTF、回折限界、及びエアリーディスクに関するセクションで解説しています。FナンバーとDOFに関する詳細は、センサーへの周辺光量 – ロールオフ (周辺減光)と口径食で解説します。

前のセクション次のセクション Next Section