赤外アプリケーションでメニスカスレンズを使用するメリット

著者: Katie Walker

TECHSPEC Germanium Meniscus Lenses

光学レンズの他のレンズ形状の多くと比較し、メニスカスレンズの在庫販売品は余り多くありません。メニスカスレンズは、小径スポットサイズに集光したり、コリメーション用途に主として用いられるのに対し、平凸レンズは優れた費用対効果を得ることができます。メニスカスレンズの使用は、平凸レンズと比べると更なる価格アップにはなりますが、十分に性能の改善が期待できるという現実があります。

球面収差

レンズの球面形状は、平行光線入射時にレンズの入射位置によって光軸上の異なる位置に焦点を結ぶという球面収差を引き起こします (Figure 1)。球面収差は、複数枚のレンズ素子を用いて他の素子を過剰補正することで補正できますが、IRシステムの多くの場合、赤外域で機能する材料の価格は、可視域で機能する材料のそれよりもかなり高価になります。そのため、追加するレンズの素子枚数を最小化することが理想です。レンズ複数枚で構成する代わりに、レンズの形状をベストフォームに変えることで、一枚レンズの使用で球面収差を最小化することが可能になります。

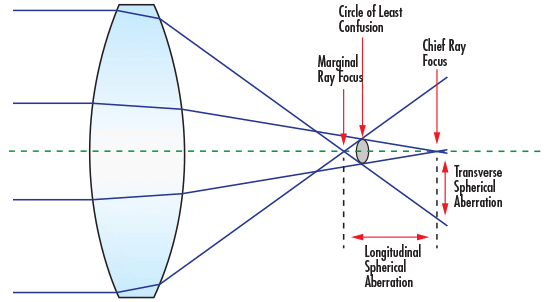
Figure 1: 球面収差

屈折率とレンズの中心厚の値が既に決まっていたとしても、特定の焦点距離を有するレンズを作り出す曲率半径の組み合わせはまだ無数に存在します。この曲率半径の組み合わせにより、異なるレンズ形状を作り出すことができ、またレンズ内を伝搬する光線の曲がり度合いが球面収差やコマ収差の生じる大きさに直接的な影響を与えます。

レンズ形状は、コディントンの形状ファクター “C” を用いて表すことができます (公式1とFigure 2 参照)。

(1)$$ C = \frac {R_2+R_1}{R_2-R_1} $$

Coddington Shape Factors for Different Lens Configurations

Figure 2: 様々なレンズ形状に関するコディントンの形状ファクター

物点を無限遠、レンズを絞り面と設定した時の薄肉レンズの収差公式を用いて、球面収差が最小となる条件を導き出すことができます (公式 2)。

(2)$$ C_\text{Min Spherical}=-\frac{ 2\left(n^2-1\right)}{n+2} $$

使用する波長が一定だと仮定すると、球面収差を最小化する屈折率 (Index of Refraction)と形状ファクター (Slope Factor)間の関係は、下図のように表すことができます (Figure 3)。

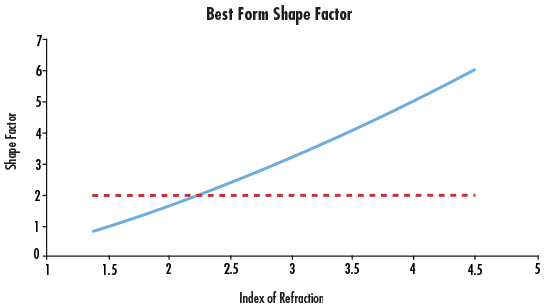
$Best Form Shape Factor as a Function of Index of Refraction$

Figure 3: 屈折率の関数としたときのベストフォーム形状

メニスカスデザインのメリット

ガラスの屈折率が通常1.5~1.7の範囲に分布する可視スペクトルアプリケーションでは、平凸レンズに近い形状が球面収差を最小化するのに最善の選択と言えます。しかしながら、屈折率が2.0を超えることも多い赤外アプリケーションにおいては、球面収差低減の観点から、メニスカスレンズの形状の方がより高いメリットを得ることができます。

球面収差の最小化は、レンズの表裏の屈折面二面で光線を同じ大きさだけ各々曲げた時に達成されます。ゲルマニスムメニスカスレンズの屈折面第一面では、比較可能な同材料の平凸レンズよりも少しだけ大きく光を曲げます。これに対して、第二面側では平凸レンズの方がメニスカスレンズよりも相当量大きく光を曲げます。このアンバランスさにより、レンズ全体として捉えると、平凸レンズによる球面収差の量の方がより大きくなります。

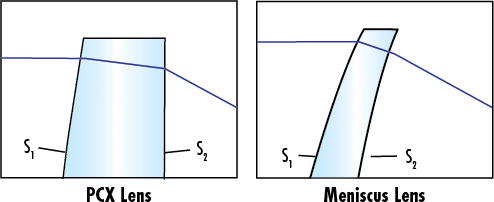
φ25 x f50mmのゲルマニウム平凸レンズと同ゲルマニウムメニスカスレンズの性能比較をFigure 4にまとめました。平凸レンズの方がメニスカスレンズよりもレンズ屈折面で光をより大きく曲げてしまうことが容易に見て取れます。この曲がり度合いの増加が球面収差の増加を引き起こします。ゲルマニスムメニスカスレンズは、得られる集光スポットサイズを劇的に小さくし、要求の厳しいIRアプリケーションでの使用により適します。

Diagram of 25 x 25mm Germanium PCX Lens versus 25 x 25mm Germanium Meniscus Lens

	平凸レンズ	メニスカスレンズ
S₁面での球面収差量	0.1λ	2.4λ
S₂面での球面収差量	14.2λ	2.9λ
レンズ全体での球面収差量	14.3λ	5.3λ
集光スポットサイズ	258μm	83μm

Figure 4: φ25 x f50mmのゲルマニウム平凸レンズと同ゲルマニウムメニスカスレンズの図表

メニスカスレンズは可視域で使用しても性能は向上しますが、製造コストの増加分を鑑みると、一般的にそのメリットは十分と言えません。Table 1は、φ25 x f50mmのフッ化カルシウム (CaF₂) 製平凸レンズと同スペックのメニスカスレンズの可視スペクトルでの性能、及びφ25 x f50mmのゲルマニウム (Ge)平凸レンズと同スペックのメニスカスレンズの赤外スペクトルでの性能を比較したものです。ゲルマニウムレンズは、メニスカス形状のものを使用したときにスポットサイズの大幅な減少が見られます。