変調伝達関数入門
光学設計者が光学系の性能を比較しようとするとき、一般的に使用される指標は変調伝達関数 (Modulation Transfer Function; MTF) です。球面シングレットレンズのようなシンプルな部品にも、またテレセントリックレンズのようなレンズ複雑枚構成の組みレンズであっても、MTFは用いられます。MTFの有意性を理解するために、MTFの構成要素、重要性、特徴など、MTFを定義する一般的な原則と実例を考察します。
MTFの構成要素
変調伝達関数 (MTF) を適切に定義するには、まず、画像の性能を正確に特徴付けるために必要な2つの用語、即ち、解像力とコントラストを定義する必要があります。
解像力
解像力とは、被写体の細部を区別するイメージングシステムの能力です。通常は、1ミリメートル当たりのラインペア数 (一対の等幅の黒線と白線) で表されます。この1ミリメートル当たりのラインペア数の単位 $ \small{\left(\tfrac{\text{lp}}{\text{mm}}\right)} $ は、周波数としても知られています。周波数の逆数により、2本の解像された線の間隔をミリメートル単位で得ることができます。白と黒のバーが等間隔で交互に並んだテストターゲット (1951 USAF ターゲットやロンキー・ルーリングなど) は、システム性能をテストするのに最適です。テストターゲットの詳細な説明は、テストターゲットの正しい選定をご覧ください。すべてのイメージングオプティクスにおいて、このようなパターンを撮像すると、完璧な輪郭の線が幾分かボケます (Figure 1) 。高解像イメージでは、ボケが最小限に抑えられる結果、細部まで詳細に再現された画像になります。逆に、低解像イメージでは、細部の再現が欠けています。
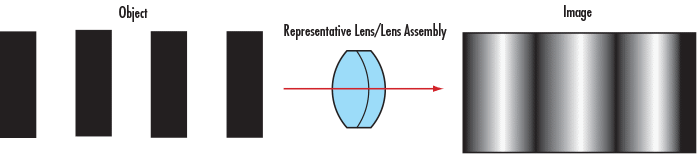
Figure 1: 低解像力のイメージングレンズを通過する前の完璧なラインエッジ (左) と通過後のラインエッジ (右)
ラインペアを理解するための実用的な方法は、ラインペアをカメラセンサー上の画素として考えることです。カメラセンサー上では、一組のラインペアは2画素分に相当します (Figure 2) 。解像度の各ラインペアを再現するには、2つのカメラセンサー上の画素が必要 - 一つの画素が赤線用、他方の画素が空白スペース用 - になります。前述の例えを用いるなら、カメラの画像解像度は、画素サイズの2倍に等しいと規定できるようになります。
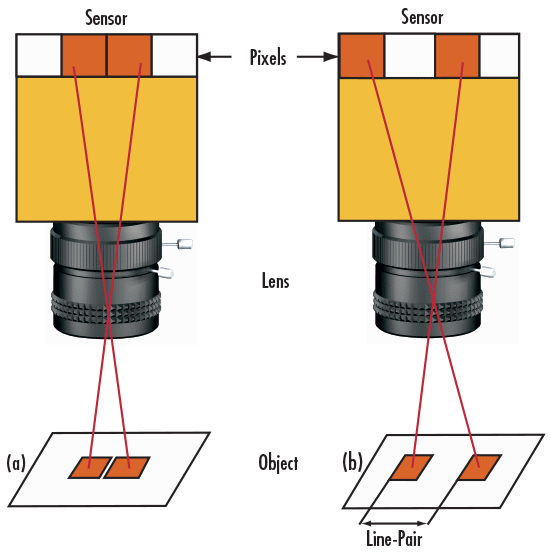
Figure 2: ラインペアが解像されない場合 (a) と解像された場合 (b) のイメージングシナリオ
これに対応し、物体側の解像度は、カメラの解像度とイメージングレンズの光学倍率 (PMAG) で計算されます (式1-2)。なおこれらの式は、イメージングレンズが解像力を低下させないという前提に基づいたものであることに留意する必要があります。
コントラスト/変調
白のバーを最大値に、そして黒のバーをゼロ値に割り当てることで、バーターゲットの強度を正規化することを検討してみます。これらの値をプロットすると方形波が得られ、コントラストの概念がよりわかりやすくなります (Figure 3)。数学的に、コントラストは次式 (3) で計算されます:
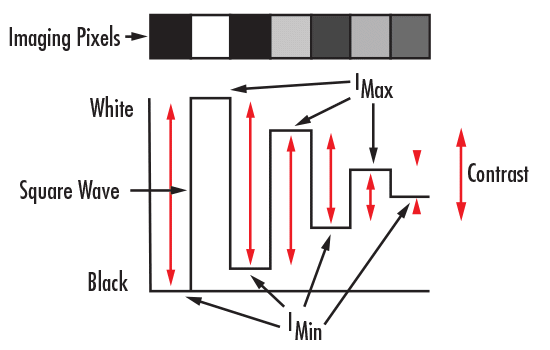
Figure 3: 方形波で表されるコントラスト
Figure 1でのイメージングの例に同様の原理が適用されると、イメージング前後の強度パターンを見ることができます (Figure 4)。コントラストまたは変調は、最小および最大強度値が物体面から像面に伝達される際の忠実度として定義することができます。
コントラストと画質の関係を理解するために、イメージングレンズをFigure 1で用いたものと同じ解像力のものであると考え、より高いラインペア周波数での物体の撮像をFigure 4に図解します。Figure 5は、ラインの空間周波数がさらに高くなり、画像のコントラストが低下する様子を図解します。同じ解像力のイメージングレンズを使用する場合、常にこの現象が存在します。画像を鮮明に表示するためには、黒が真の黒で、白が真の白で、その間のグレースケールは最小限である必要があります。
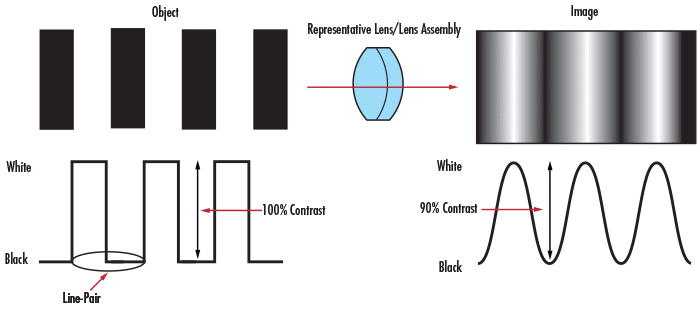
Figure 4: バーターゲットとその画像のコントラスト
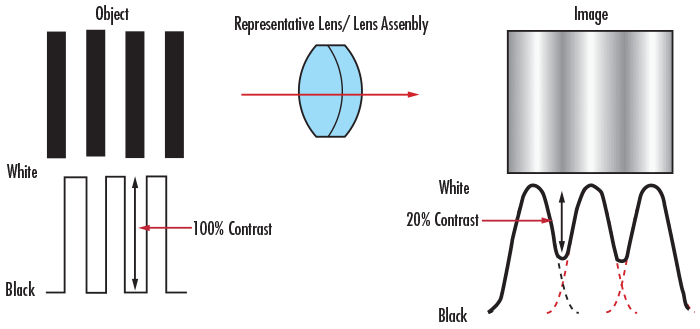
Figure 5: 物体面 (左) と像面 (右) でのコントラスト比較
イメージングアプリケーションでは、イメージングレンズ、カメラセンサー、および照明が、最終的な画像コントラストを決定付けるのに重要な役割を担います。レンズのコントラストは、再現される物体コントラストの割合 (%) から通常定義されます。コントラストを再現するセンサーの能力は、アナログカメラではデシベル (dB)、デジタルカメラではビットで通常規定されます。
MTFの理解
変調伝達関数 (MTF) の構成要素である解像力とコントラスト/変調が定義されたので、続いてMTF自体を考えます。その名称が示すように、レンズのMTFは、特定の解像力で物体から画像へコントラストを伝達する能力の測定値です。言い換えれば、MTFは解像力とコントラストを単一の仕様に統合する手法です。テストターゲットにおける線の間隔が減少するほど (即ち、周波数が増加するほど)、レンズがこの伝達を効果的に行うことが難しくなります。その結果、MTFは周波数の増加と共に低下していきます (Figure 6)。
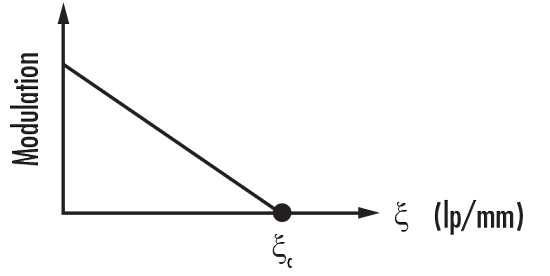
Figure 6: 収差フリーの矩形開口レンズのMTF
円形の瞳を有する収差フリーの画像に対しては、式 (4) によってMTFが計算されます。ここで、MTFは空間分解能 $\small{\left( \xi \right)}$ の関数で、システムが解像できる最小のラインペアを表します。カットオフ周波数 $\small{\left( \xi _c \right)}$ は式 (6) で計算されます。
Figure 6は、矩形の瞳を有する収差フリー画像のMTFのプロットです。予期可能な通り、空間分解能が増加するにつれて、MTFは低下しています。ただし、こうしたケースは理想化されたもので、実際には完全に収差フリーのシステムは存在しないことに留意する必要があります。
MTFの重要性
従来のシステムインテグレーション (および重要性の低いアプリケーション) では、システムの性能は最弱リンクの原則を用いて推定されます。最弱リンクの原則とは、システムの解像度は最も解像力の低い構成部品のみによって制限されるという考え方です。このアプローチは迅速な推定には非常に有益ですが、実際にはシステム内の各構成部品すべてが画像へのエラーに寄与し、最弱リンク単体よりも画質が劣るようになるため、実際には不都合があります。
システム内のどの構成部品にも固有の変調伝達関数 (MTF) があり、それが結果としてシステム全体のMTFに寄与します。この中には、イメージングレンズ、カメラセンサー、イメージキャプチャーボード、およびビデオケーブルなどが含まれます。システムの最終的なMTFは、各構成部品のMTF曲線をすべて積算したものになります (Figure 7)。例えば、ソニーの白黒カメラを用いて、f=25mmの固定焦点距離レンズと同DG シリーズ (ダブルガウス) レンズの両レンズでのシステム性能を比較してみます。システムのMTF曲線を解析することで、どちらの組み合わせが十分な性能をもたらすかを直接判断することができます。ある計測アプリケーションでは、正確な画像のエッジ検出を行うのに、ある程度のコントラストが求められます。$ 30 \tfrac{\text{lp}}{\text{mm}} $ の画像解像度で35%の最小コントラストが求められる場合、f=25mmのDG シリーズ レンズが最適の選択になります。
MTFは、解像力とコントラストの面でシステム全体の画像性能の定量化に利用できる最適なツールの一つです。結果として、システム内のイメージングレンズとカメラセンサー個々のMTF曲線を知ることで、設計者は、特定の解像力に向けて最適化する際の適切な選択を行うことができます。
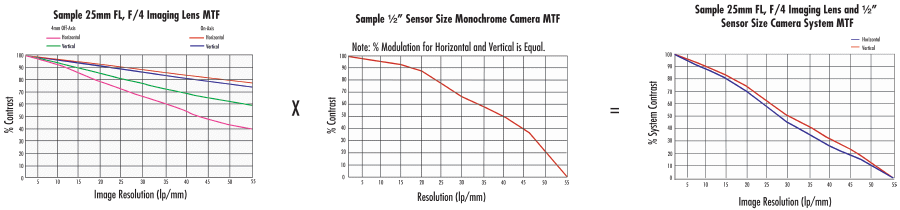
Figure 7: システムMTFは個別の構成部品のMTFになる: レンズMTF x カメラMTF = システムMTF
MTFの特徴
現実世界のMTFの決定
理論的な変調伝達関数 (MTF) 曲線は、任意のレンズの光学設計データから生成することができます。これは有益かもしれませんが、製造公差を考慮した上での現実世界での実際のレンズを表わすものではありません。形状やコーティングといったファクターは、理想的なレンズあるいはレンズシステムからはわずかに逸脱するため、製造公差は、オリジナルの光学設計に対して常に多少の性能低下をもたらします。こうした理由から、エドモンド・オプティクスの製造拠点では、MTFの定量化に必要な光学試験・測定装置への投資が行われています。このMTF試験・測定装置によって、設計したレンズおよび商用レンズ (光学設計データが非公開) の両方の実際の性能を評価することができます。結果として、以前は精密実装に使用可能なレンズは、既知のデータを有するレンズに限られていましたが、現在は商用レンズでもそれが可能になっています。
MTFグラフ/データの読み取り

MTF曲線の下の部分の面積が大きいからといって、それが必ずしも最適な選択になるとは限りません。設計者は、アプリケーションに用いられる実際の解像度に基づきそれを判断していくべきです。前述したように、MTFグラフは伝達したラインのコントラスト百分率と周波数 (本/mm) の関係を表わします。エドモンド・オプティクスが提供するMTF曲線については、次のいくつかの点に留意する必要があります:
- 各MTF曲線は、空間内の一点に対して計算されます。通常のフィールドポイントには、 軸上、70%像高、フル像高が含まれます。70%像高は、全イメージング領域の約50%分の領域に相当するため、一般的な参照ポイントになります。
- 軸外MTFデータは、タンジェンシャルとサジタル (それぞれにTとSで表す) の両方向に対して計算されます。場合によって、2つの個別の曲線ではなく、両者の平均値が示されることがあります。
- MTF曲線は、システムの共役 (倍率)、波長帯、Fナンバーなどのいくつかのファクターに依存します。一つのMTF曲線は、それぞれの指定された値で計算されます。したがって、そのパーツが特定のアプリケーションに対して機能するかを判定する前に、こうしたファクターを確認しておくことが重要になります。
- 空間周波数は、1ミリメートル当たりのサイクル数 (またはラインペア数) で表されます。この周波数の逆数により、ラインペアの間隔 (1本の黒線と1本の白線の周期) をミリメートル単位で得ることができます。
- 名目MTF曲線は、光学設計プログラムで利用可能な標準の設計データ情報を用いて生成されます。この設計データ情報は、当社のウェブサイトやカタログ、およびZemax®用に用いられる当社のレンズカタログでも見つけることができます。この名目MTFは、ベストケースシナリオを表わすものであり、製造公差は考慮されていません。
MTFを概念的に把握することは難しいことかもしれません。物体面から像面にコントラストを伝達する概念を理解する最も簡単な方法は、現実世界の例を用いることなのかもしれません。Figure 8-12では、f=25mmの2つの固定焦点レンズのMTF曲線と画像の比較 - グリーンシリーズ M12 マウントレンズ (#54-855) とCシリーズ 固定焦点レンズ (#59-871) です。この2つのレンズの多色回折MTFをFigure 8に示します。試験条件によっては、両レンズは同等の性能を生み出すことができます。この具体例では、両レンズともUSAF 1951 解像力ターゲット上のグループ数2、ライン数5 – 6 (Figure 10で赤枠で図示) 、およびグループ数3、ライン数5 – 6 (Figure 10で青枠で図示) の解像を試みています (Figure 9) 。ターゲット側の実際のサイズは、グループ数2、ライン数5 – 6が6.35 – $ 7.13\tfrac{\text{lp}}{\text{mm}} $ (14.03 - 15.75μm)、グループ数3、ライン数5 – 6が12.70 – $ 14.25 \tfrac{\text{lp}}{\text{mm}} $ (7.02 - 7.87μm) です。当社の1951 USAF 解像力計算ツールを用いてライン数とグループ数を指定することで、解像力周波数を簡単に得ることができます。
同じ試験パラメーター下では、#54-855よりも#59-871 (より良いMTF曲線を有する) のほうが優れた画像性能を生み出すことは明らかです (Figure 11-12)。こうした特定の1951 USAF 周波数を使った現実世界の例では、より高い空間周波数でより高い変調値を持つ方が、より鮮明な画像になります。しかしながら、これは常に当てはまるというわけではありません。一部のレンズは、より低い空間周波数を非常に正確に解像でき、非常に低いカットオフ周波数を持つようにデザインされています (換言して、空間周波数が高くなると解像することはできない)。標的にするグループ数が-1、ライン数が5-6の場合、より低い周波数での変調値を勘案すると、2つのレンズは、より類似した画像を生成するはずです。
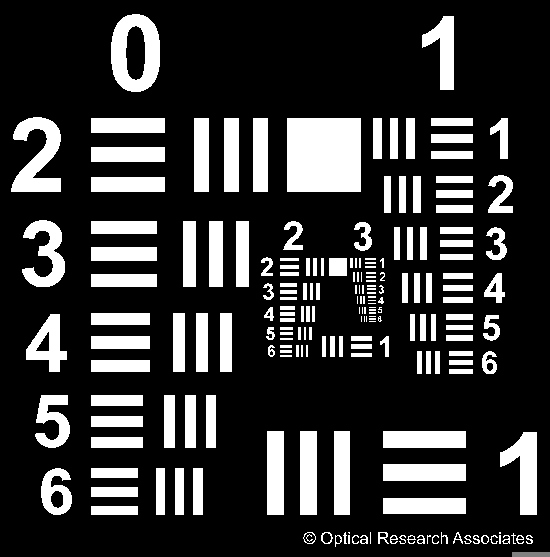
Figure 9: USAF 1951 解像力ターゲット

Figure 11: USAF 1951 解像力ターゲット上のグループ数 2、ライン数 5-6 を解像する#54-855 グリーンシリーズ M12 マウントレンズ (左) と#59-871 Cシリーズ 固定焦点レンズ (右) の比較

Figure 12: USAF 1951 解像力ターゲット上のグループ数 3、ライン数 5-6 を解像する#54-855 グリーンシリーズ M12 マウントレンズ (左) と#59-871 Cシリーズ 固定焦点レンズ (右) の比較
変調伝達関数 (MTF) は、画質を測定する最も重要なパラメーターの一つです。光学設計者やエンジニアは、とりわけ特定の被写体がどれだけ正確に撮像されるかで成否が決まるアプリケーションでMTFデータを頻繁に参考にします。MTFを本当の意味で把握するには、まず解像力とコントラストの概念、また物体の画像が物体面から像面にどのように伝達するかを理解する必要があります。最初は難しく感じるかもしれませんが、MTFデータを理解し、最終的に解釈することは、いずれの光学設計者にとっても非常に強力なツールになります。知識と経験を伴うことで、MTFは、数多くの製品の中から適切なレンズを選定することを遥かに容易にしてくれます。
参考文献
- Dereniak, Eustace. "OPTI 340 - Optical Design." Lecture, The University of Arizona, Tucson, AZ, Spring 2010.
- Geary, Joseph M. "Chapter 34 – MTF: Image Quality V." In Introduction to Lens Design: With Practical Zemax Examples, 389-96. Richmond, VA: Willmann-Bell, 2002.
- Smith, Warren J. "Chapter 15.8 The Modulation Transfer Function." In Modern Optical Engineering, 385-90. 4th ed. New York, NY: McGraw-Hill Education, 2008.

































もしくは 現地オフィス一覧をご覧ください
クイック見積りツール
商品コードを入力して開始しましょう
Copyright 2023, エドモンド・オプティクス・ジャパン株式会社
[東京オフィス] 〒113-0021 東京都文京区本駒込2-29-24 パシフィックスクエア千石 4F
[秋田工場] 〒012-0801 秋田県湯沢市岩崎字壇ノ上3番地