光学収差の比較
光学収差の存在は、完全な数学的モデルからの逸脱を意味します。収差は、物理的、光学的、あるいは機械的な欠陥によって引き起こされるのではないことを理解しておくことが重要です。むしろ、光の波としての性質から、レンズの形状自体、あるいはシステム内の光学素子の配置によって引き起こされます。光学系は、結像面でのサイズやその位置を把握するために、近軸理論を用いて設計されるのが一般的です。近軸理論では、収差は考慮されていません。光を波としてではなく、光線として扱うため、収差を引き起こす波としての現象を無視しています。光学収差に関する序論として、色収差と単色光学収差をお読みください。
色収差と単色光学収差の異なるグループや種類を理解した後、コンピュータ解析や現実世界を通じてシステム内にその存在を認め、次にその残存量を減らしながらシステムを補正していきますが、その作業は容易なことではありません。一般に、光学設計者はZemax® や Code V®といった光学設計ソフトウェアの中に対象の光学系を入れ、その性能や収差を事前把握します。それでも、光学部品が実際に作られ、その系を組み立てた後にその出力結果を確認すると、収差がまだ認められる場合があることも理解しておく必要があります。
光学的に収差を識別する
一つの光学系内にどの収差が存在しているかを決定することは、コンピュータ解析段階においてでも常に容易な作業ではありません。なぜなら、どんな系にも共通して複数の異なる収差が同時に存在しているからです。光学設計者は、コンピュータ生成のスポットダイグラム やOPDファンプロットダイアグラム (光路長差図)、そしてレイファンプロットダイグラム (横収差図)を始めとする様々なツールを駆使して収差を認識し、それを補正しようと試みます。スポットダイグラムは、一つの光の点が対象光学系を通して像を結んだ時にどのように現れるかを解説します。OPDファンプロットダイアグラムは、平坦な波形に対して波打った形状になり、完全な波であればx軸方向に沿って平坦な形状となります。レイファンプロットダイグラムは、光軸方向の収差を瞳座標の関数として表したものです。以下に紹介したメニュー画面は、タンジェンシャル面 (垂直y方向)とサジタル面 (水平x方向)に対する代表的なOPDファンとレイファンプロットダイグラムで、$ \small{H = 1} $時の次にあげる収差をそれぞれ表します。関心のある収差を選択して、各図形の違いをご確認ください: チルト $ \left( \small{W_{111}} \right) $, デフォーカス $ \left( \small{W_{020}} \right) $, 球面 $ \left( \small{W_{040}} \right) $, コマ $ \left( \small{W_{131}} \right) $, 非点 $ \left( \small{W_{222}} \right) $, 像面湾曲 $ \left( \small{W_{220}} \right) $, ディストーション $ \left( \small{W_{311}} \right) $
収差名 (波面係数):

Figure 1: エアリーディスクパターン
収差を認めること、とりわけ設計段階においてそれを認めることは、補正するための第一歩です。光学設計者はなぜ収差を補正したがるのでしょう? その回答は、可能な限り性能の最も高い光学系、即ち回折限界性能のシステムを創作することにあります。回折限界のシステムでは、含有する全ての収差が、エアリーディスクのスポットサイズ、即ち円形開口によって引き起こされる回折パターンのサイズの中に収まります (Figure 1)。
公式1は、システムに用いられる波長をλ、システムのFナンバーをf/#とした時のエアリーディスクスポットサイズ (d) を計算するのに用いられます。
光学収差の実例
ある光学系を設計かつ製造後、例えばレーザーのような点光源をその系に通し、一つの点が像面上でどのように現れるかを確認することで、収差の存在を把握することができます。複数の収差が同時に現れることもありますが、一点のスポット像に近づけば近づくほど、生じている収差量は一般に少なくなります。これは、そのスポットが系によって拡大されるサイズに関係なく、です。以下に挙げた7つの例は、当該収差がその系で唯一存在する場合の光線の様子の図解と、共通して用いられるテストターゲット (Figures 2 - 4)をその系に使用した時のシミュレーション画像、そしてその収差を最小化するために検討可能な是正手段を紹介したものです。
シミュレーション画像はCode V®を用いて作られ、当該収差をよりわかりやすく見せるために多少誇張しています。なおここで述べている収差は、その共通性という点から、一次と三次の光学収差のみです。より高次の収差の補正は、画質のわずかな改善を行うのにもとても複雑な作業になります。

Figure 2: 固定周波数パターンのグリッドディストーション図票

Figure 3: ネガパターンの1951 USAF 解像力ターゲット

Figure 4: スターターゲット
| チルト収差 – $\small{W_{111}}$ | |
 Figure 5a: チルト収差の図解 |
 Figure 5b: チルト収差のシミュレーション画像 |
性質
|
是正手段
|
| デフォーカス収差 – $\small{W_{020}}$ | |
 Figure 6a: デフォーカス収差の図解 |
 Figure 6b: デフォーカス収差のシミュレーション画像 |
性質
|
是正手段
|
| 球面収差 – $\small{W_{040}}$ | |
 Figure 7a: 球面収差の図解 |
 Figure 7b: 球面収差のシミュレーション画像 |
性質
|
是正手段 |
| コマ収差 – $\small{W_{131}}$ | |
 Figure 8a: コマ収差の図解 |
 Figure 8b: コマ収差のシミュレーション画像 |
性質
|
是正手段
|
| 非点収差 – $\small{W_{222}}$ | |
|
Figure 9a: 非点収差の図解 |
 Figure 9b: 非点収差のシミュレーション画像 |
性質
|
是正手段
|
| 像面湾曲 – $\small{W_{220}}$ | |
 Figure 10a: 像面湾曲の図解 |
 Figure 10b: 像面湾曲のシミュレーション画像 |
性質
|
是正手段
|
| ディストーション – $\small{W_{311}}$ | |
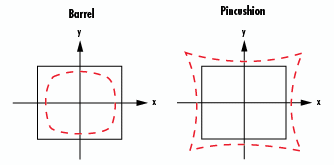 Figure 11a: ディストーションの図解 |

Figure 11b: 樽型ディストーションのシミュレーション画像 
Figure 11c: 糸巻き型ディストーションのシミュレーション画像 |
性質
|
是正手段
|
光学収差を認識することは、光学系においてそれを補正する上でも大変重要です。その目標は、対象のシステムを回折限界にまで持っていくことにあります。光学やイメージングシステムは、複数の異なる収差を同時に持つことがありますが、各収差が色を伴うものなのか、或いは単色性のものなのかで分類することができます。設計段階において、例えば開口絞りの位置を変えたり、光学レンズの種類を変えるなどを行い、収差の発生数や発生度合いを顕著に減らし、事前に補正しておくことがベストです。全体的にみれば、光学設計者は一次や三次の光学収差を主として減らすことにのみ従事します。より高次の収差を減らすことは、画質のわずかな改善を行うのにもとても複雑な作業となるためです。
参考文献
- Dereniak, Eustace L., and Teresa D. Dereniak. Geometrical and Trigonometric Optics. Cambridge: Cambridge University Press, 2008.



























もしくは 現地オフィス一覧をご覧ください
クイック見積りツール
商品コードを入力して開始しましょう
Copyright 2023, エドモンド・オプティクス・ジャパン株式会社
[東京オフィス] 〒113-0021 東京都文京区本駒込2-29-24 パシフィックスクエア千石 4F
[秋田工場] 〒012-0801 秋田県湯沢市岩崎字壇ノ上3番地