変調伝達関数 (MTF)

レンズの性能を理解して計算することは難しい場合があります。回折、光学収差、設計上の基準や哲学、製造上の公差やエラーを始め、レンズの性能に影響を与える数多くの変数があります。最善のシステム性能を得るには、光学設計者と最終ユーザーの両方が、計測されたレンズ性能を表示するのに用いられるメトリクスにアクセスできる必要があります。計測されたこのレンズ性能は、変調伝達関数 (MTF) 曲線の形で用意されます。

変調伝達関数 (MTF)

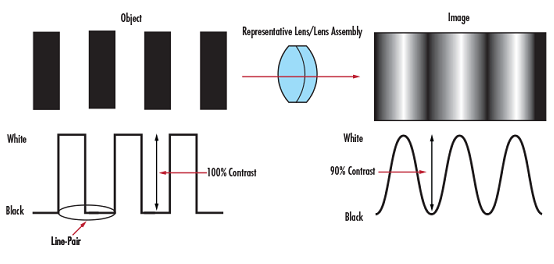
変調伝達関数 (Modulation Transfer Function; MTF)曲線は、空間周波数 (解像度)が変化する時、レンズがそのコントラストをどのように再現するかを反映した情報の濃密な性能曲線です。この曲線は、アプリケーションニーズに応じて注目される特定基本パラメータにおいて、光学的収差が性能にどのような影響を及ぼすかを検討する際の参考データとしても利用されます。ビジョンシステムでは、基本パラメータを始めとして、何かしらの設定を変更すると、性能曲線の形状も変わってしまうことを理解しておくことも重要です。レンズと撮像の基本パラメータは、イメージングの基本に定義されています。

Figure 1にMTF曲線の共通的なスタイル – 縦軸に光学伝達関数 (コントラスト)、横軸に空間周波数 (解像度)をプロット – を紹介しています。空間周波数がどのように決定されるかは、解像力で網羅しています。この曲線は、特定の作動距離、Fナンバー、センサーサイズ、波長域におけるレンズ性能の大観を表わしています。MTF曲線は、解像度力とコントラストの情報を同時に示すため、複数のレンズをアプリケーション要件に応じて評価し、互いを比較することができます。MTF曲線を正しく使用すると、アプリケーションが実行可能かどうかを判断するのに用いることができます。

An MTF performance curve illustrates contrast vs. frequency.

Figure 1: MTF性能曲線はコントラストと空間周波数の関係を表わす

MTF曲線にはいくつかのスタイルがありますが (例えば周波数別のMTFやフィールド別のMTFなど)、一般的と思われる周波数別のMTFを複数の色の曲線 (黒、青、緑、赤) を用いてFigure 1に紹介します。一番上方にある黒の実線は、レンズの回折限界時の曲線を表わし、レンズ性能の理想的限界を再現しています。レンズ性能をどのように改善しようと試みても、この線より上側にプロットされることは絶対にありません。その他の色の線は、全てこの回折限界曲線よりも必ず下側にプロットされ、実際のレンズのMTF曲線を再現しています。各々の線は、異なるフィールド像高 (センサー上のポジション)に対応しています。下記曲線サンプルの場合、3種類の異なるフィールド像高がプロットされています：青色の軸上曲線は、イメージサークル中心部でのMTF特性を表わし、緑色の70%像高曲線は、イメージエリア全体のおおよそ半分の位置におけるMTF特性を表わしています。最後に、赤色のフル像高曲線は、イメージセンサーのコーナーサイドにおけるMTF特性を表わします。なおサンプルによっては、より多くのフィールド像高をプロットしたMTF曲線も存在します。

曲線内に見られるその他の注目すべきポイントに、TとSのアルファベットで記述された破線と実線状の曲線の性能差があります。Tは焦点のタンジェンシャル面 (yz面方向) を表し、Sはサジタル面 (xz面方向) を各々表します。この2つのフィールドは、光学面の非対称性によって生じる光学収差 (非点収差など) が原因で互いの面の焦点位置が異なってしまうために存在します。このことは、光軸上においてはタンジェンシャルとサジタルの2つの性能曲線に分かれないことも意味しています。この変動は、フィールドスポットが他の方向よりも一つの方向によりすばやく混ざり、同一周波数で異なる軸に異なるコントラストレベルを生成させます。特定のアプリケーションに対してレンズを評価するときは、この2つの線の低い方の影響を考慮していくことが重要です。システムで最高レベルの性能を得るためには、センサー全体のコントラストレベルを最大化していくことが一般的に有利です。レンズ素子が傾いていたり、偏芯が存在したりすると、非対称性がそこに生じ、光軸上にもTとSの異なる曲線が現れることになりますが、これはMTFカーブでは示されません。 MTF曲線の詳細については、アプリケーションノートの変調伝達関数入門をご参照ください。

前のセクション次のセクション Next Section