ディストーション

ディストーションという光学収差は、時に画質を低下させる収差と見なされることがあります。技術的に言えば、他の光学収差が画像情報をミックスして像ボケを作り出してしまうのに対し、ディストーションの場合は、画像情報を実際に減らしているのではなく、物体の位置的情報のみに誤差を与えている固有の収差と考えられます。他の光学収差によって画像情報そのものが失われ、その修復が容易に行えないのに対し、ディストーションの場合はその量を算出した上で後から補正することができます。他の光学収差に関する詳細は、収差で解説しています。なお、ディストーションの量が極端に大きな環境では、画像情報の一部が失われることがあります。これは、倍率変化による解像力の変化や、センサーの各画素で解像できない量の情報が入射してしまう場合に起こります。

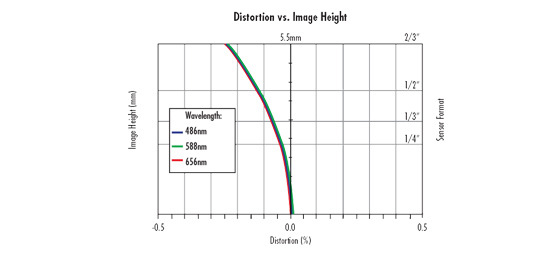
ディストーションは単色収差の一つで、特定作動距離で得られる実視野内での画像の倍率的変化を表わします。これは、精密なマシンビジョンやゲージ用途において極めて重要です。ディストーションは、作動距離によって倍率 (実視野)の大きさが変わる視差とは全く異なるものです (視差に関する詳細は、テレセントリシティが有利な点内のテレセントリシティのセクションで解説しています)。ディストーションは、Figure 1に示した通り波長によって大きさが変わるため、マシンビジョンシステムにおいてディストーションを取り除き補正する場合は、照明に用いる波長を考慮する必要があります。Figure 1のような色毎にプロットした曲線は、どれだけの量のディストーションを取り除くかを判断する際にとても役立ちます。

他の光学収差と同様、ディストーションの量はレンズの光学設計で決まります。一般的に、広い実視野が得られるレンズほどディストーションの量も大きくなります。ディストーションは、薄レンズで計算できる3次収差の一つで、その大きさはフィールド像高の3乗に比例します。これは、実視野の大きいレンズ (低倍率または焦点距離が短い)は、実視野の小さいレンズ (高倍率または焦点距離が長い)よりもディストーションの量が多くなる傾向にあることを意味します。特に焦点距離の短いレンズによって広い実視野サイズを得ている場合は、マシンビジョンシステム内に生じる光学収差 (ディストーション等)が大きくなります。これに対し、テレセントリックレンズは、ディストーションの量が一般的に極めて少なく、同システムに広く採用されます。なお、最小限のディストーションしか持たないレンズを設計する際は、実現可能な限界解像力を妥協する必要があるかもしれないことにも気付くことも重要です。解像力を高い次元で維持しながらディストーションを最小化するには、レンズ枚数を増やしたり、或いは特殊な光学特性を有する一般に高価な硝材を利用したりする必要があります。

A distortion plot showing the variance of distortion with respect to wavelength.

Figure 1: ディストーション特性は波長によって変動する

ディストーションの大きさはどのように規定する？

ディストーションの大きさは、像高に対する百分率で通常規定されます。もし測定体制が導入されていない場合、ビジョンシステムには通常±2~3%のディストーションがあると考えられます。ディストーションには、正と負の2種類があります。正値となる樽型のディストーションは、実視野内のどのポイントも、中心部により近付く距離で像を結びます。負値となる糸巻き型のディストーションは、逆に中心部からより遠ざかる距離に像を結びます。樽型と糸巻き型の名称は、真四角のフィールドを各々のディストーション特性のレンズで撮像した時にどのような形状に変化するかに由来しています (Figure 2参照)。

An illustration of positive and negative distortion.

Figure 2: 正と負のディストーションの図解

ディストーションの大きさは、本来像を結ぶべき距離 (Predicted Distance; PD)と実際に像を結んだ距離 (Actual Distance; AD)の関係から単純に計算することができます (式 1参照)。距離の算出は、ドットグリッド状のテストパターンを使うことで行います。

(1)$$ D \left( \% \right) = \frac{\text{AD} - \text{PD}}{\text{PD}} \times 100 \% $$

(1)

$$ D \left( \% \right) = \frac{\text{AD} - \text{PD}}{\text{PD}} \times 100 \% $$

レンズには正か負のディストーションがありますが、画像内で正と負の値が混在することもあります。加えて、波長が変わるとディストーションの大きさも変わります。最後に、レンズの作動距離が変わると、ディストーションの大きさも変わります。システムからディストーションを取り除いて高次の精度を得るためには、究極的にそのアプリケーションに応じて使用するレンズを個々に検討していくことがとても重要です。

ディストーション曲線の例

Figure 3は、負の (樽型の) ディストーション特性を有するf=35mmレンズのディストーション曲線です。この例では、どの波長でもほぼ同じレベルのディストーション特性であることがわかり、波長に関連する問題がないことがわかります。

Negative, or barrel, distortion in a lens.

Figure 3: レンズの負の (樽型の)ディストーション

対するFigure 4の場合は、興味深い特性が見て取れます。始めに、3色の曲線が異なる軌道を描き、ディストーションのレベルが波長ごとに異なっていること、次に、正と負の両方のディストーションがレンズ内に存在することです。この波または口ひげのような形状の軌道を描くディストーション曲線は、計測やゲージ用のレンズなど、非常に低レベルのディストーションを持つようデザインされたレンズに多く見られます。この例で複数の異なる波長を同時に用いるアプリケーションの場合、システム校正してディストーションを取り除くための特別な配慮が求められます。

A wave, or mustache, distortion in a lens.

Figure 4: 波または口ひげのような軌道を描くレンズのディストーション

重要な違い：光学ディストーションとTVディストーション

レンズのデータシートには、次の2つのディストーションの種類のどちらかが通常記載されています。光学ディストーションとTVディストーションです。光学ディストーションは、レンズにより得られた歪みを含む実際の画像と本来あるべき歪みを全く含まないパーフェクトな画像間の距離的違いを相対百分率で表わしています。このディストーションは、ドットグリッドパターン状のテストターゲットを用いて実測することができます。テストターゲットの中心から実視野内の各ドットまでの距離を測定することで、本来あるべき各ドット位置との距離の差を求め (Figure 5参照)、式 1に沿って光学ディストーションの大きさを定量化することができます。

Calibrated target (red circles) vs. imaged (black dots) dot distortion pattern.

Figure 5: ディストーション用テストパターンを用いて撮像した実際の画像 (黒ドット)と本来映るべきパターン (赤丸)との比較

TVディストーションの測定は、米国RIAAの画像標準規格によって規定されており、正方形状のテストターゲットを用いて実視野の垂直方向の画面いっぱいにまで映るようレンズで撮像することで求められます。撮像した正方形状チャートのコーナー部と端面中央部間の高さの違いから、式 2に沿ってTVディストーションを求めることができます。TVディストーションは、画像端面部に映る一本線がどの程度真っ直ぐに映るかを定量化したもので、一つのフィールドポイントだけで捉えてみれば、光学ディストーションの考え方と基本変わりません。

(2)$$ D_{\small{\text{TV}}} \left( \% \right) = \frac{\Delta H}{H} \times 100 \% $$

()

$$ D_{\small{\text{TV}}} \left( \% \right) = \frac{\Delta H}{H} \times 100 \% $$

ただ、フィールド内の一点だけでディストーションの大きさを規定してしまっているため、ディストーションが0%となる中間地点が存在したとしても一義的に判断してしまうことが考えられます。Figure 4には、どの波長においてもディストーションが0%の地点が存在します。ただ、フル像高で捉える場合、ディストーションがゼロでないのも事実です。TVディストーションの一例をFigure 6に紹介します。

TV distortion with both barrel and pincushion distortion.

Figure 6: 樽型 (左図)と糸巻き型 (右図)のTVディストーション

Figure 4で示したように、複数枚のレンズを使用して組み立てられた組みレンズを用いた現実世界においては、ディストーション曲線は必ずしも単調な軌跡のものばかりではなく、実視野内で正や負の符号が変わるものもあります。これは、なぜ光学ディストーションでプロットした方のがTVディストーションよりも好まれるかの理由を示す好例です。規定方法の違いから、同一レンズをTVディストーションで計測した値は、光学ディストーションで得られる最大数値よりも遥かに低くなることがあります。そのため、アプリケーションに最も適応するレンズを選定する際は、そのレンズがどちらのディストーションで規定されたものなのかを理解することがとても重要になります。

キーストーン歪み (台形歪み)

レンズの光学設計に起因するこれまでのディストーションに加え、システムのアライメントが不適切な場合、視差から生じるキーストーン歪み (台形歪み)を持つことがあります (Figure 7参照)。

An example of keystone distortion in a lens layout (a) and as it manifests in in the image plane (<em>b</em>)

Figure 7: レンズレイアウトにおけるキーストーン歪みの例 (a) とそれが画像平面に現れる例 (b)

イメージングシステムのディストーションを補正する際、キーストーン歪みは、光学ディストーションと同様に考慮されるべき内容です。ディストーションは、見た目に影響を及ぼす収差の一つと考えられますが、正しいレンズを選定する際は他のシステムの仕様と同様に注意深く考慮されるべきです。但し、ディストーションを補正するアルゴリズムの導入は、追加の工程時間と労力が必要になり、高速や組み込みアプリケーションでは許容できない場合もあります。

前のセクション次のセクション Next Section