非球面レンズのイレギュラリティとストレール比

全ての光学系は、回折限界として知られる理論的な性能限界があります。ストレール比は、光学系の現実の性能を回折限界性能と比較する際に用いられるスペックです。非球面レンズや他の集光用オプティクスでは、ストレール比は製造されたオプティクスのピーク集光スポット強度と回折限界ピーク強度の比として定義されます (Figure 1)¹。非球面レンズの製造技法が異なると、独自の面誤差を与え、ストレール比に違いを与えます。この影響を理解するために、非球面を正しく規定して過剰なスペックや余計なコストの発生を防ぎ、所望するスペックになるのを確実にしていくことが重要です。Fナンバーの小さいファストな非球面レンズではこれがとりわけ重要で、伝統的な研削研磨で製造される非球面は、他の方法で作られるものよりも影響を受けます。業界標準の閾値は、ストレール比が0.8より大きいレンズを“回折限界”として分類しています。

Figure 1: 25mm径、F2の非球面レンズの588nmにおける集光スポットの放射断面形状。出来上がったレンズのストレール比は0.826で、回折限界の基準に適合する

ストレール比は、下記近似式で用いられるRMS透過波面誤差とも関連し、σはRMS波面誤差でλが単位になります²。この近似式は、透過波面誤差が<0.2λの時に有効になります³。

ストレール比のイレギュラリティの影響

オプティクスのストレール比は、面のイレギュラリティ、即ち光学面の名目形状からのずれに大きく依存し、面のイレギュラリティは用いる製造方法で決まります。球面光学素子はオーバーサイズの工具を用いて研磨されるのが一般的で、これによって光学面上に低空間周波数誤差を与えます。しかしながら、非球面レンズ製造ではサブアパーチャーの研削と研磨法を利用するのが一般的で、より複雑なイレギュラリティ構造を作り出します。規定された面のイレギュラリティとその根本的な構造の関係を理解することで、レンズ性能とその結果生じるストレール比の洞察が可能になります。

例えば、空間周波数への影響を考えてみます。面のイレギュラリティが回転対称のコサイン関数としてモデル化される場合、結果として得られるストレール比は、RMS値での面不規則性の関数として、様々なコサイン周期で調べることができます (Figure 2と Figure 3)。

Figure 2: 非球面レンズ製造においてコサインパターンが起こった典型的な面イレギュラリティ誤差。25mm径のF2非球面レンズ上のラジアルコサインイレギュラリティマップで、コサイン周期は左から20mm, 10mm, 5mm

Figure 3: 面イレギュラリティのRMS値が等しい場合、非球面の開口全体を占めるコサイン周期数が大きくなるほど、ストレール比は小さくなる

ここで大切な要素は、コサイン周期をmm単位ではなく、レンズ開口全体での周期の数として見ることです。非球面製造に用いられるサブアパーチャーツールでは、非球面の直径が小さくなるほど、径の大きな非球面に比べてストレール比の低下が少なくなります。

ストレール比に対する面の不規則性の影響は、レンズのFナンバーにも依存します。一般則として、より明るい非球面レンズになるほど、即ち非球面レンズのFナンバーが小さくなるほど、ストレール比に対する面のイレギュラリティの影響はより大きなものになります。Figure 4 は、F2レンズとF0.75レンズの比較 (どちらも25mm径) ですが、特定コサイン周期ではレンズがより明るくなると、暗いレンズと比較してストレール比の低下がより大きくなるのがわかります。

Figure 4: コサイン周期が等しい場合、明るい非球面 (Fナンバーが小さい) は暗い非球面 (Fナンバーが大きい) と比較すると、性能劣化がより大きくなるのが破線と実線の比較からわかる

パワースペクトル密度とイレギュラリティスロープ

上記の例に基づき、イレギュラリティをマッピングした空間周波数成分は、レンズのストレール比に影響を与えることは明らかです。PV値、あるいはRMS値のイレギュラリティに加え、この空間周波数にはその他のスペックが要求されることがあります。

空間周波数を直接的に評価するのに用いられるスペックの一つにパワースペクトル密度 (PSD) と呼ばれるものがあります⁴。PSDは、面のイレギュラリティを空間周波数の関数として評価し、ある空間周波数範囲からの影響を制限するのに用いることができます。また、全ての空間周波数を同時に抑えるのにも用いられることがあります。

高い空間周波数での不規則性を抑えるよりシンプルかつ効果的な方法は、PV値に加え、面のイレギュラリティマップを形成するコサイン関数のスロープを抑えることです。PV値でのイレギュラリティ限界が等しい場合、スロープの傾斜がより高くなることは、面上のより高い空間周波数側に関連してきます (Figure 5)。スロープの大きさは、最大RMSスロープ値で与えられることも多く、単純な最大スロープ要求よりもレンズ面をより包括的に評価することになります⁵。スロープ誤差は、積分長 (integration length) と呼ばれる規定された横方向距離で定義されます (Figure 6)。製造時のスロープと理想的スロープ間の差が積分長全体にわたって平均化されます。例えば，スロープの仕様は「1mmの積分長に対して0.07mrad」のように与えられます。スロープは、積分長のすべてのデータポイントに対する最良の線形フィットとして定義されるか、あるいは単純に積分長範囲内の最初と最後のデータポイント間の差で定義されます。

Figure 5: 面のイレギュラリティマップに対して最大スロープのスペックが規定されている場合、表面上のより高い空間周波数成分の影響を減らす閾値を作り出す

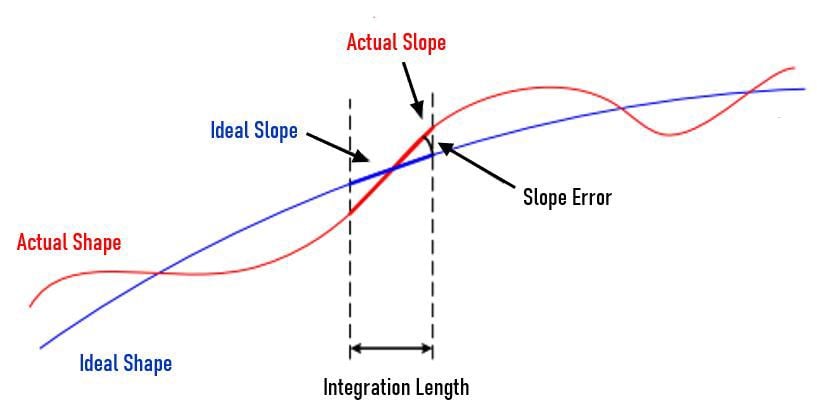
Figure 6: スロープ誤差は積分長全体にわたる実際のスロープと理想的スロープ間の角度差になる⁶

面のイレギュラリティの空間周波数は、ストレール比や非球面性能に大きな影響を与えます。周期が小さくなるほど、ある面イレギュラリティでのストレール比の低下は大きくなります。レンズ面のイレギュラリティマップの形状は、それ自体でのイレギュラリティのスペックだけでなく、それが性能に与える真の影響を理解するのに必要となります⁷。Fナンバーが小さくなることも、性能低下をより大きくさせます。

参考文献

1. Strehl, Karl W. A. “Theory of the telescope due to the diffraction of light,” Leipzig, 1894.
2. Mahajan, Virendra N. "Strehl ratio for primary aberrations in terms of their aberration variance." JOSA 73.6 (1983): 860-861.
3. Smith, Warren J. Modern Optical Engineering. 4th ed., McGraw-Hill Education, 2007.
4. Lawson, Janice K., et al. "Specification of optical components using the power spectral density function." Optical Manufacturing and Testing. Vol. 2536. International Society for Optics and Photonics, 1995.
5. Messelink, Wilhelmus A., et al., "Mid-spatial frequency errors of mass-produced aspheres," Proc. SPIE 10829, Fifth European Seminar on Precision Optics Manufacturing, 7 Aug. 2018, doi:10.1117/12.2318663.
6. Ceyhan, U. (2013). Characterization of aspherical lenses by experimental ray tracing [Doctor of Philosophy in Electrical Engineering thesis]. Jacobs University.
7. Kasunic, Keith J., Laser Systems Engineering, SPIE Press, 2016. (ISBN 9781510604278)

前のセクション 次のセクション