光学基板の熱的特性

熱膨張係数

温度変動を受けやすいアプリケーションには、アサーマルな光学系が開発されなければなりません。アサーマル光学系は、環境の熱的変化に影響を受けず、結果としてピントずれとは無縁になります。材料の熱膨張係数 (Coefficient of Thermal Expansion; CTE) と温度による屈折率変化 $ \left( \tfrac{\text{d} n}{ \text{d} T} \right) $ に依存するアサーマルデザインの開発は、赤外線領域でとりわけ重要になります。

CTEは、温度変化に対する材料のサイズの変化の割合を表す尺度です。熱膨張は、次式にように定義されます：

$ \small{\alpha_{L}}$ is the linear CTE, $ \small{L} $ is the length in one dimension, $ \small{T} $ is the temperature, and $ \tfrac{\text{d} L}{\text{d} T} $ is the reciprocal of the temperature gradient with respect to the $ \small{L} $ dimension. 

 $ \small{\alpha_{A}}$ is the area CTE, $ \small{A} $ is the area in two dimensions, and $ \tfrac{\text{d} A}{\text{d} T} $ is the reciprocal of the temperature gradient with respect to the area. 

 $ \small{\alpha_{V}}$ is the volumetric CTE, $ \small{V} $ is the volume in three dimensions, and $ \tfrac{\text{d} V}{\text{d} T} $ is the reciprocal of the temperature gradient with respect to the volume. For isotropic materials including most glass and metal, the relationship between CTEs is shown in Equation 4.

In practice, notably for small temperature changes, the differential terms for the change in length and change in temperature ($\small{\text{d}L}$ and $\small{\text{d}T}$ respectively) are typically well-approximated by differences ($\small{ \Delta L}$ and $\small{ \Delta T}$ respectively) seen in Equation 5.

(5)$$ \alpha_L \approx \frac{1}{L} \frac{\Delta L}{\Delta T} $$

一般的には、物体が加熱されると、その構成分子の運動エネルギーが増加するので、物体が膨張します (Figure 1)。しかしながら、中には温度と長さが逆比例となる例外も稀ながら存在します。例えば水のCTEは、3.983℃以下では負の値となり、3.983℃以下では温度が下がると膨張します。

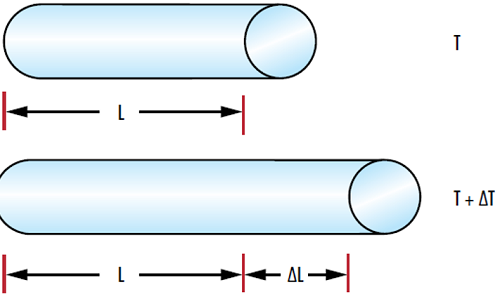
Figure 1: 温度変化 $ \left( \small{ \Delta T \small} \right) $ が材料の熱膨張係数 (CTE) に起因する材料の長さの 変化 $ \left( \small{ \Delta L} \right) $ につながる

The linear CTE is given in units of $ \tfrac{1}{ ˚ \text{C}}$ or $ \tfrac{1}{ \text{K}}$. When selecting an optic for your application, linear CTE is important to consider because changes in the optic’s size may influence alignment and stresses on the component. In environments involving swings in temperature, users need to be cognizant that their optics will not expand when heated. An optic that is 25mm at room temperature may be 25.1mm at 300˚C, which could break the mounting or skew light in an unwanted direction, thereby affecting pointing stability or laser alignment; this is generally why a small linear CTE is desired.

屈折率の温度係数

屈折率の温度係数 $ \left( \tfrac{\text{d} n}{\text{d} T} \right) $ は、温度に対する屈折率変化の尺度です。大抵のIR材料の$ \tfrac{\text{d} n}{\text{d}T} $は、可視光用のガラス材料のそれよりも桁数が大きく、屈折率に大きな変化が生じます。 Whether the refractive index of glasses increases or decreases with increasing temperature depends on the specific material, but most glass types will have higher refractive indices at higher temperatures.¹ When designing athermalized lenses, glasses with both positive and negative temperature coefficients are paired together to balance out the refractive index change of each other.

材料の$ \tfrac{\text{d} n}{\text{d}T} $は、次式により与えられます：

ここで、

$ \small{ T_0 }$は参照温度 (20℃)

$\small{T}$は温度 (単位は℃)

$\small{\Delta T}$は$ \small{ T_0 }$からの温度差

$\small{\lambda}$は光の波長

$ \small{D_0, D_1, D_2, E_0, E_1,} $および$ \small{\lambda} _{\small{\text{TK}}} $は材料の定数

反射型オプティクスの$ \tfrac{\text{d} n}{\text{d} T} $は、薄膜の屈折率変化によるごくごくわずかな性能変動を除いて重要な特性とは言えません。しかしながら、透過型オプティクスの$ \tfrac{\text{d} n}{\text{d} T} $の場合は、温度変化時の安定性を見極めるのに重要な特性と言えます。ハイパワーレーザービームが光学部品に入射する際は吸収がある程度は必ず起こり、温度上昇になりますが、$ \tfrac{\text{d} n}{\text{d} T} $の大きさは、これがどの程度性能に影響を及ぼすかの見極めになります (Figure 2)。

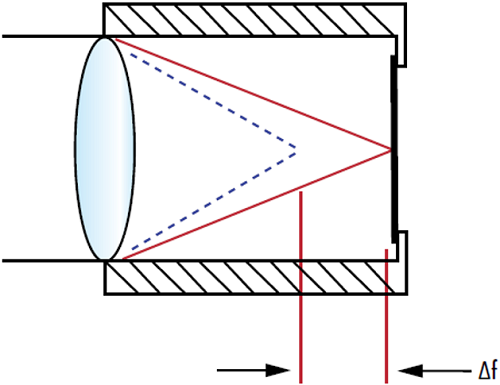
Figure 2: 光学部品の温度による屈折率の変化 $ \left(  \tfrac{\text{d} n}{\text{d} T} \right) $ は、レンズの焦点距離シフト $ \left( \Delta f \right) $ に繋がり、焦点位置が変わることになる

熱伝導率

材料の熱伝導率 $ \left( \small{k} \right) $ は、その材料の伝導による伝熱能力の尺度です (Figure 3)。$ \tfrac{\text{W}}{ \left( \text{m}  \,  \cdot \, \text{K} \right)} $ もしくは $ \tfrac{\text{Btu}}{\left( \text{hr} \, \cdot \, \text{ft} \, \cdot \, \text{˚F} \right)} $の単位が通常用いられ、その大きさを以下の式で定義されます：

ここで、$ \small{Q} $は時間$ \small{t} $の間に伝導する熱量を表し、$ \tfrac{Q}{t} $の単位は$ \tfrac{\text{J}}{\text{s}} $もしくは$ \small{\text{W}} $ になります。$ \small{A} $は基板の断面積、$ \small{\Delta T} $は材料の一方の面と他方の面間の温度差、$ \small{d} $は材料の厚さです。

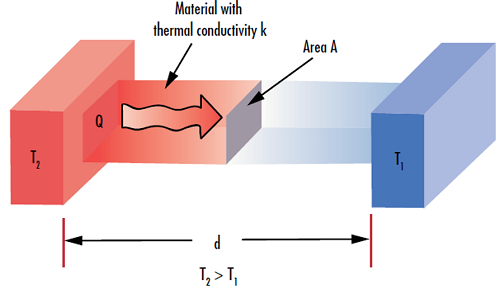
Figure 3: 材料の熱伝導率 $ \left( \small{k} \right) $ は、熱量 $ \left( \small{Q} \right) $ が既定の厚さ $ \left(  \small{d} \right) $ を通過する際の伝導能力を定義する

金属のような高い熱伝導率をもつ材料は、ガラスやプラスティックなどの低い熱伝導率をもつ材料よりも遥かに早く熱を逃がすことができます。光学部品にレーザー放射を透過させる主要な効果の一つに放射エネルギーの熱エネルギー変換があるため、材料の熱伝導率を知っておくことは光学部品周りのエネルギーバランスを評価する上で重要になります。特定の波長を反射または透過しない材料は、光をより多く吸収してすぐに熱せられます。カラーガラスフィルターや吸収型のフィルターはその典型例です。光学部品が蓄熱して非定常的になると、とりわけ効果的な冷却システムを用いていない場合は、損傷がすぐに起こります。仮に冷却されていたとしても、熱伝導が一様ではない不均質な光学部品の場合は材料内にホットスポットが発生し、部品の損傷がすぐに、そしてより確実に発生することになります。屈折率の温度係数と同様に、熱伝導率を理解することは、ハイパワーレーザーシステムのモデル化とどのような光学的性能の効果を期待するかを考える上で重要になります。

参考文献

1. “TIE-19: Temperature Coefficient of the Refractive Index.” Schott, July 2016.